Lab 10
The purpose of this lab is to implement grid localization using Bayes filter.
Bayes Basics
The Bayes filter uses a combination of a control input, measurements from sensors, and then establishes a belief of where the robot currently is. After every input (tell the robot to move somewhere), there is a probability that the robot is actually at the location and also a non-zero probability that the robot is at a different state. The Bayes filter tries to converge on the actual position by making a prediction and then continuosly updating based on the previous position. The basic algorithm for the Bayes filter is shown below.

Compute Control
The computation consists of three parts: the first is a rotation in the direction of the new location, then a linear translation to the new location, then finally a second rotation to correct the robot's orientation. The calculation is shown below.

Odomoetry Motion Model
This code uses a gaussian distribution to determine the probability that the robot actually moved based on the input control. This process is repeated for each movement described above, and then the probabilities are multiplied together to get an overall probability. The code is shown below.

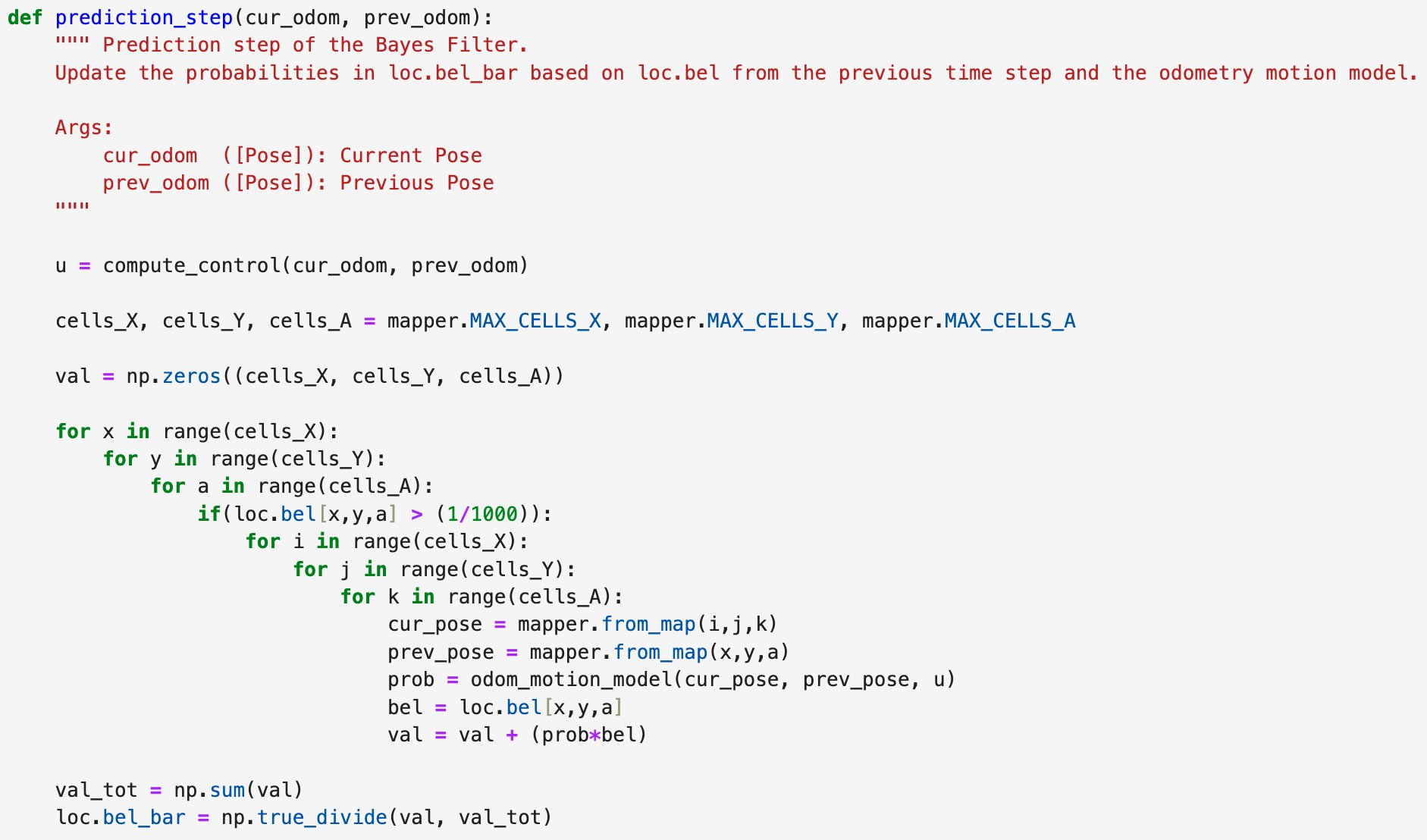
Prediction Step
The prediction code predicts the probability that the robot will be at some state given its belief it was at the previous state and underwent the given control input. Rather then setting a belief of 0 to 0, I used a value of 0.0001 in order to prevent issues with the probabilities. The code is shown below.
Sensor Model
This function runs through 18 different measurements to determine the probability of a sensor measurement given the current position. Overall, this code defines the probability that is used in other functions. The code is shown below.

Update Step
This function takes the predicted belief (bel_bar), and it updates the belief based on the sensor input value. This is done by multiplying the probability from the measurement and the predicted belief state. Then, the value is normalized to keep the sum of the probabilities equal to one. The code is shown below,

Simulation Results
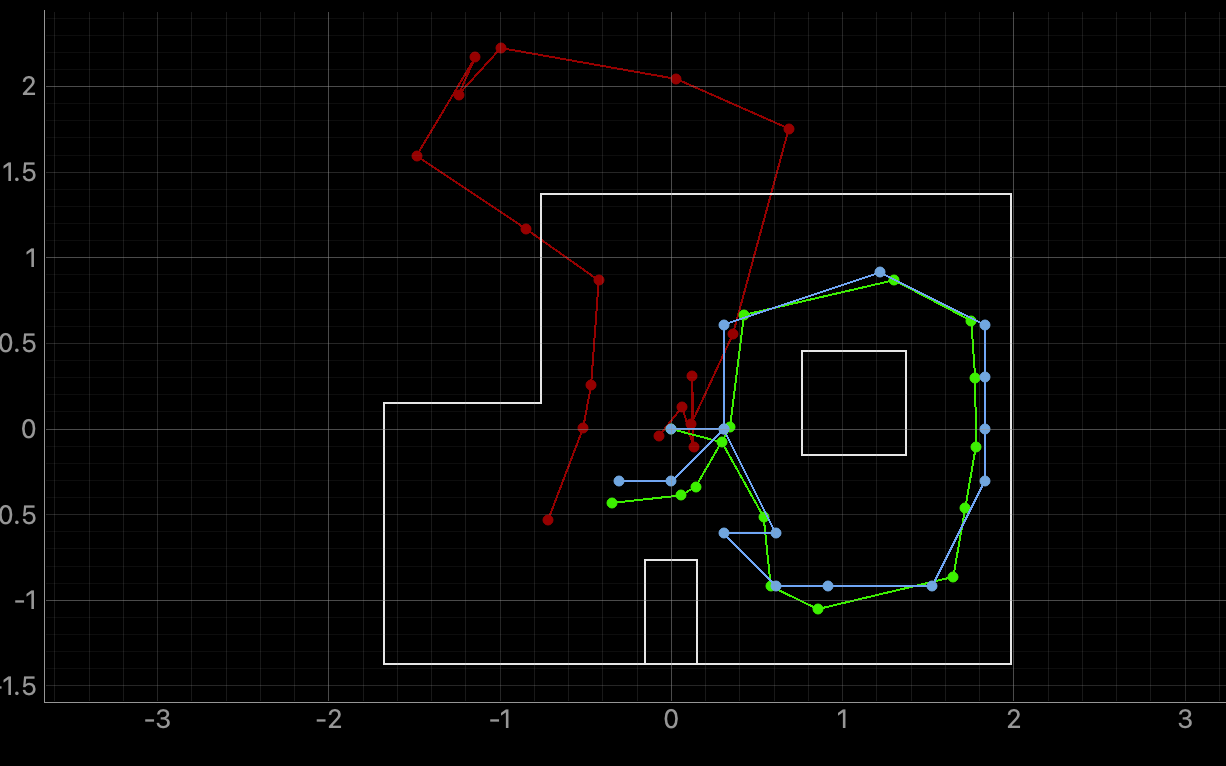
The simulation results are shown below. The odomoetry model (shown in red) is very inaccurate. However, the true results (shown in green) and the belief results (shown in blue) are pretty close. This means that the prediction from the Bayes filter is pretty good and converges nicely. While the filter did stray a little at a few of the points, it was able to get itself back on track quickly.
Lab 10 Takeaways
I learned a lot about Bayes filter and its possible implications for my robot. I look forward to implementing it in the next lab to help with physical localization.